Осевая симметрия
Использование этого расчётного модуля целесообразно для решения вращательно-симметричных задач. Этому предположению должны удовлетворять и геометрия конструкции, и нагрузки. Подходящим примером может послужить решение задачи вертикальной нагрузки одиночной сваи, круглой выемки, или откачка подземной воды из круглой скважины.
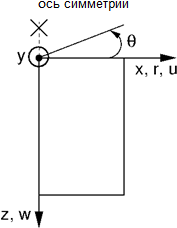Предпосылка осевой симметрии
Подобно задаче плоской деформации речь идёт об общей трёхмерной проблеме, которую можно преобразовать в решение двумерной задачи (см. рис.). Решение будет отнесено к 1 м длины дуги радиусом x(r). Ось симметрии всегда представляет начало координаты x(r). Сдвигающими составляющими деформации в направлении ротации можно пренебречь. Наряду с составляющими напряжения и деформации в плоскости сечения принимаем во внимание также образование периметрической нормальной составляющей напряжения и деформации. Соответствующие ненулевые составляющие напряжения и деформации можно сложить в вектор напряжения и деформации следующим образом:
Очевидно, что периметрическая составляющая деформации, а следовательно, также задействованные нормальные составляющие напряжения приобретают на оси симметрии бесконечные значения. С точки зрения аппроксимации методом конечных элементов для повышения точности их определения необходима достаточно густая сетка кругом оси симметрии.
Внимания заслуживает также приложение линейной и плоской нагрузки. Отдельные примеры нагружения поверхности территории представлены на следующем рисунке. Очевидно, что эффект от таких нагрузок увеличивается с увеличением расстояния от оси симметрии. Следовательно, приложение нагрузки такого типа непосредственно на ось симметрии не скажется на расчёте. В таком случае необходимо выбрать тип нагружения оси симметрии. Программа позволяет нагружение только сосредоточенной силой.
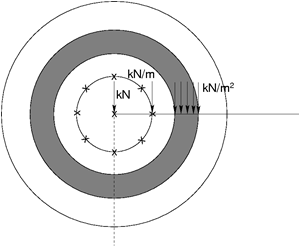Примеры пригрузки рельефа
У балочных элементов имеем дело с задачей плоской ротационно-симметричной оболочки с влиянием изгибающих воздействий. Ненулевые степени свободы аналогичны примеру пояса пластин, принятого для решения задачи плоской деформации. Наряду с осевыми (меридиальными) воздействиями необходимо принимать во внимание также оболочечные и изгибающие воздействия в периметрическом направлении (см. следующий рисунок).
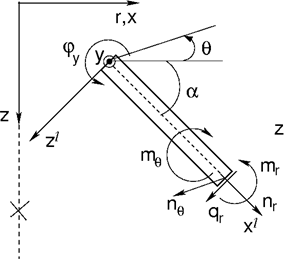Балочный элемент в осевой симметрии
Соответствующие составляющие внутренних сил (см. рис.), отнесённые к 1 м ширины можно сложить в вектор напряжения следующим образом:
В случае круговой пластины или кругового кольца (угол α = 0) можно говорить о радиальных и периметрических составляющих внутренних сил (см. следующий рисунок).
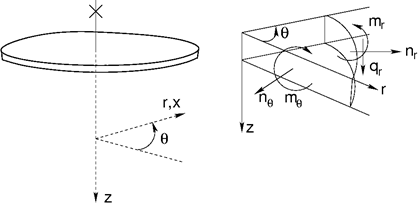Внутренние силы на круговой пластине
Отношение между внутренними силами и соответствующими составляющими деформации могут быть в общем случае записани в виде:
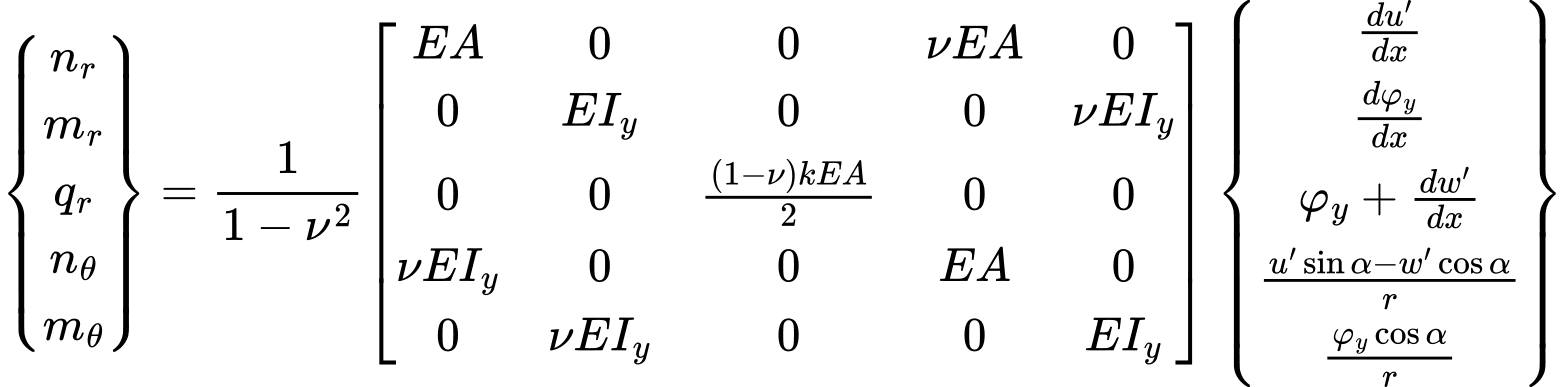
Принимаем радиус r равным бесконечности и переходим к проблеме плоской деформации. Стоит обратить внимание на обстоятельство, что у сдвигающих сил их величина, в отличие от проблемы плоской деформации, находится в сильной зависимости от плотности разбивки балки на элементы. То же самое касается вертикальных реакций.
Замечение по движению потока
Напомним, что таким же образом как реакции при анализе напряжения, значения сосредоточенных потоков в узлах сетки с нормированными поровыми давлениями тоже отнесены к 1 м длины дуги радиусом x(r). В случае плоской деформации соответствующие значения сосредоточенных потоков отнесены к 1 м длины. Этому соответствуют и общие значения расходов, которые можно определить по сосредоточенным потокам [м3/сутки/м] следующим образом:
Плоская деформация
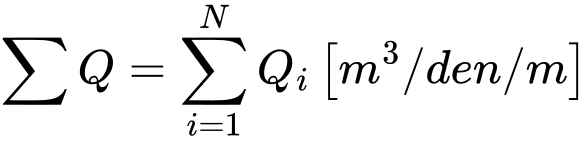
Осевая симметрия
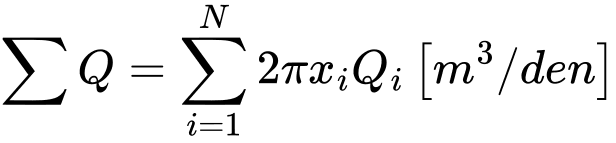
где N - количество узлов на соответствующей линии сетки, в которых рассчитывают сосредоточенные потоки Qi [м3/сутки/м]. В случае осевой симметрии представляет xi значение x-координаты данной точки, т.е. общий расход [м3/сутки] напр., через цилиндрическую поверхность (вертикальная линия) или через круглоцилиндрическую поверхность (горизонтальная линия).