Расчёт Винклер-Пастернака коэффициентов
Коэффициенты Винклер-Пастернака C1, C2 вычисляются в программе из условия равных матриц гибкости бесконечно жёсткого отдельного ленточного фундамента, опирающегося на упругий подстилающий слой.
Материал слоя характеризуется следующими параметрами:
Edef | - | модуль деформации [MPa] |
ν | - | коэффициент Пуассона |
Eoed | - | Одометрический модуль [MPa] |
G | - | модуль сдвига [MPa] |
Из них, Edef и ν независимы, а два других определяются отношениями:
![]()
и
![]()
Ленточное основание имеет ширину 2b а зона деформации под ленточным основанием имеет толщину H.
Под решением упругого основания мы подразумеваем нахождение зависимости между смещением и нагрузкой ленточного основания в виде:
![]()
где P - матрица гибкости.
Решая для изотропного однородного эластичного слоя под суженной частью фундамента, избегая при этом горизонтальных смещений, получаем матрицу гибкости P вида:
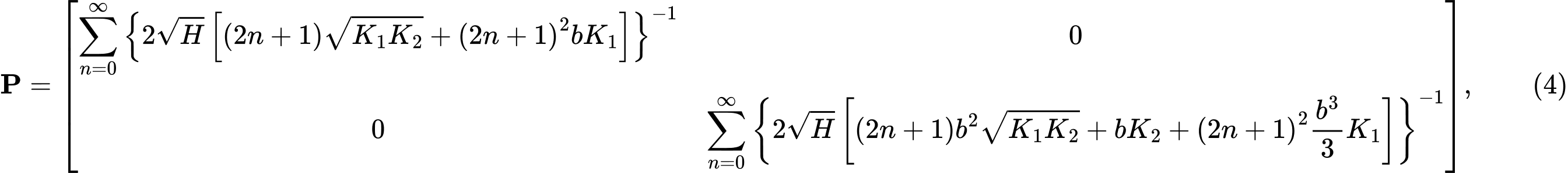
где
![]()
и
![]()
Решая дифференциальное уравнение для двухпараметрической модели подстилающего слоя, получаем матрицу P вида:
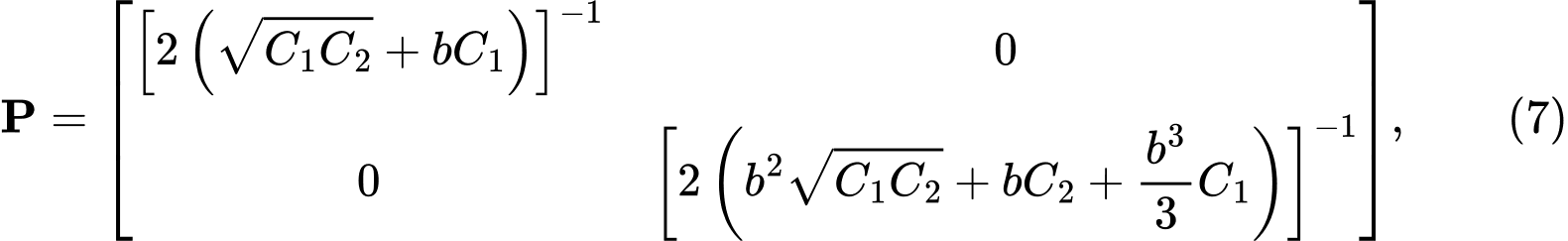
где C1, C2 - коэффициенты Винклера-Пастернака для модели подстилающего слоя. Мы находим их значения из условия, что матрица P выражения (4) должна быть идентична матрице P выражения (7). Путём сравнения и преобразования получаем соотношения:
![]()
и
![]()
где
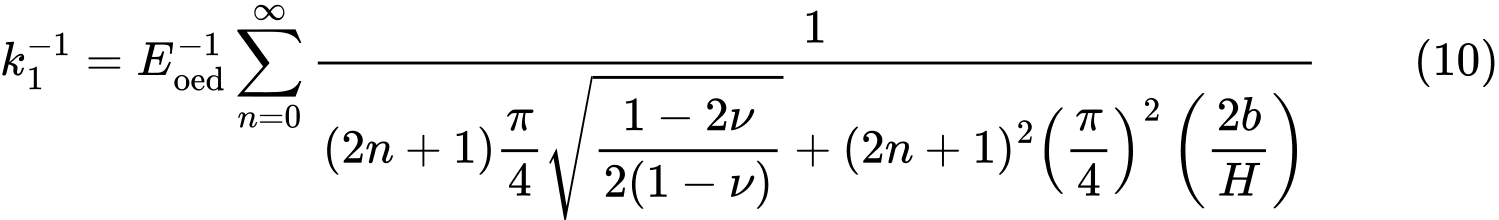
и
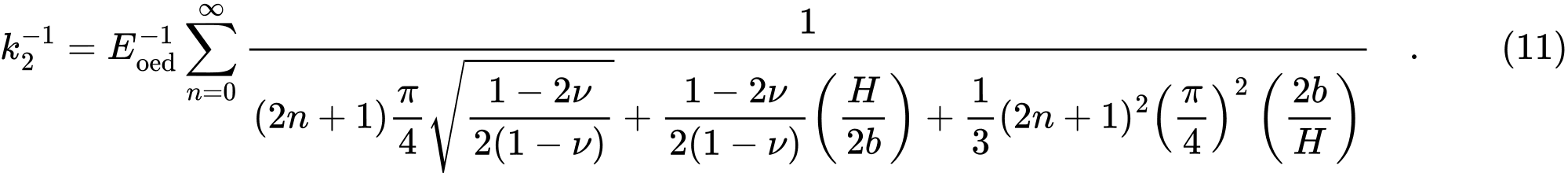
Из соотношений (8) и (9), непосредственно вычисляются значения C1 и C2, в то время как бесконечные суммы в выражениях (10) и (11) выполняются в Geo5 для первых 21 сложений.
Литература: Kuklík, P.: Příspěvek k řešení vrstevnatého podloží, Pozemní stavby, 7-1984