Modelo Drucker-Prager
El modelo de material de Drucker-Prager es el modelo de material más simple que se puede adoptar para modelar una respuesta no lineal de los suelos. A diferencia del modelo de Mohr-Coulomb, la superficie de fluencia de Drucker-Prager es suave y en el espacio de esfuerzos principal se representa como un cono cilíndrico. Como se desprende de la figura siguiente, la superficie de fluencia, de manera similar al modelo de Mohr-Coulomb, depende de la tensión efectiva media σmeff. La versión actual del modelo implementado en GEO5 MEF se basa en el supuesto de extensión triaxial. En otras palabras, la proyección de la superficie de rendimiento fDP en un plano desviador pasa por vértices internos del hexágono de Mohr-Coulomb, θ = - 30°, donde θ es el ángulo Lode.
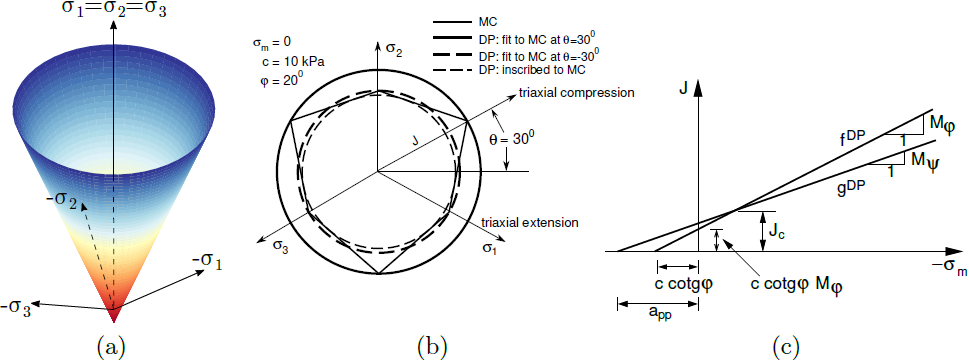 a) superficie de rendimiento en el espacio de tensiones principales, b) proyección en planos desviatorios y c) meridianos
a) superficie de rendimiento en el espacio de tensiones principales, b) proyección en planos desviatorios y c) meridianos
El modelo de Drucker-Prager permite tener en cuenta la dilatancia del material (evolución de las deformaciones plásticas volumétricas positivas durante el cizallamiento plástico) introduciendo el ángulo de dilatación ψ. La evolución de las deformaciones plásticas está controlada en general por el potencial plástico gDP. Mientras que la pendiente de la superficie de rendimiento en el plano meridiano está dada por el ángulo de fricción interna Mφ = Mφ(φ), La pendiente de la superficie del potencial plástico depende del ángulo de dilatación Mψ = Mψ(ψ). La condición ψ = φ corresponde a la regla de flujo asociada, de lo contrario se considera la regla de flujo no asociada. Más detalles se pueden encontrar en el manual teórico. Debido a que el suelo finalmente llega al llamado estado crítico (incremento cero de la deformación plástica volumétrica durante el cizallamiento plástico), es deseable limitar el grado de dilatación. Esto requiere la introducción del ratio de vacío máxima emax, para lo cual se espera alcanzar el estado crítico ψ = 0. A continuación se presenta un ejemplo ilustrativo aquí. Se presenta aquí cómo la elección del valor del ángulo de dilatación influye en la predicción de la respuesta del suelo en comparación con su comportamiento real. Para mayor claridad presentamos, en la siguiente figura, una representación gráfica de la evolución de la deformación volumétrica con corte de dilatación.
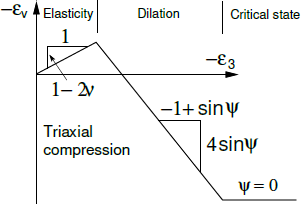 Evolución de la deformación plástica volumétrica con corte de dilatación
Evolución de la deformación plástica volumétrica con corte de dilatación
Los parámetros básicos del material que definen el modelo Drucker-Prager se enumeran en la siguiente tabla. Estos parámetros se pueden adoptar al realizar análisis en condiciones de drenaje o en el caso de condiciones sin drenaje., Tipo (1): Análisis de tensiones efectivas (cef, φef). Al elegir el Tipo (2): Análisis de tensiones efectivas (Su) El valor de cohesión eficaz c se reemplaza por el valor de la resistencia al corte no drenado Su. El valor del ángulo efectivo de fricción interna φ = φu se establece en cero, φ = 0. La superficie de fluencia de Drucker-Prager se reemplaza luego por la superficie de fluencia de Mises, véase más abajo. Sin embargo, se supone que los parámetros de rigidez son efectivos. En condiciones sin drenaje, generalmente se espera que el suelo no experimente dilatación. El ángulo de dilatación ψ = 0 Por lo tanto, se adopta para ambas opciones.
De la tabla de parámetros del material se desprende que el modelo Drucker-Prager, de manera similar al modelo elástico modificado, considera una respuesta diferente del suelo en la carga primaria y en la descarga/recarga introduciendo el módulo de descarga/recarga. Eur, véase también el modelo de Mohr-Coulomb.
Símbolo | Unidad | Descripción | |
| [MPa] | Módulo de elasticidad | |
| [MPa] | Módulo de descarga/recarga | |
| [-] | Coeficiente de Poisson | |
| [kPa] | Coeficiente de cohesión efectivo | |
| [°] | Ángulo efectivo de fricción interna | |
| [°] | Ángulo de dilatación | |
| [kN/m3] | Peso a granel | |
| [-] | Ratio de vacío inicial correspondiente al estado al final de la 1ª etapa de cálculo | |
| [-] | Ratio máximo de vacío para terminar la dilatación (cuando se limita la dilatación) | |
| [1/K] | Coeficiente de expansión térmica (teniendo en cuenta los efectos de la temperatura) |
Al elegir condiciones sin drenaje Tipo (3): análisis en tensión total Su la superficie de rendimiento de Drucker-Prager se reemplaza nuevamente por la superficie de rendimiento de Mises. De manera similar, La superficie de rendimiento de Mohr-Coulomb se reemplaza por la superficie de rendimiento de Tresca. En la figura se proporciona una representación gráfica. Esta opción considera por tanto φ = ψ = 0, que corresponde a la regla de flujo asociada. Dado que se modela un material volumétricamente incompresible, el valor del coeficiente de Poisson normalmente se selecciona en el rango de (0.49 - 0.499). Señale, que establecer el valor del coeficiente de Poisson demasiado cerca de 0,5 puede generar inestabilidades numéricas. En el mejor de los casos, los resultados serán bastante inexactos. Puede encontrar más información en el manual teórico.
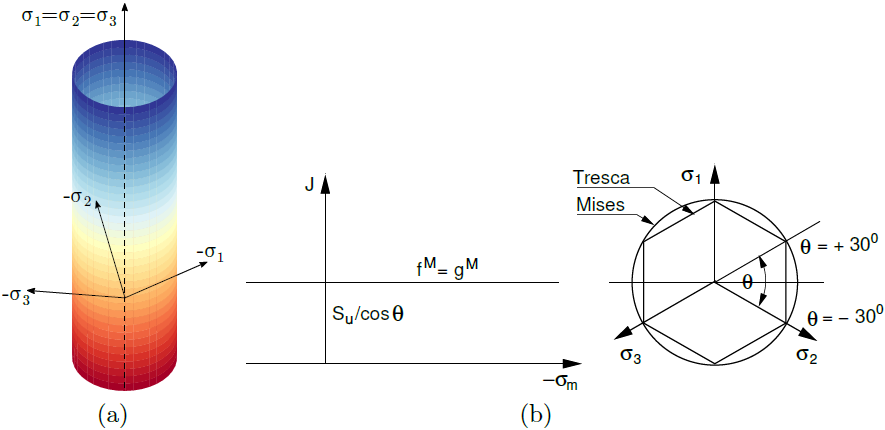 a) superficie de rendimiento en el espacio de tensiones principales, b) proyección en planos desviatorios y c) meridianos
a) superficie de rendimiento en el espacio de tensiones principales, b) proyección en planos desviatorios y c) meridianos
Los parámetros del material que definen Mises sobre la superficie de rendimiento de Tresca están disponibles en la siguiente tabla. En el caso de la superficie de rendimiento de Mises, el valor del ángulo de Lode θ es constante igual a θ = ± 30°.
Símbolo | Unidad | Descripción | |
Eu | [Pa] | Módulo de elasticidad no drenado | |
Su | [Pa] | Resistencia al corte sin drenaje | |
ν | [-] | El coeficiente de Poisson se supone en el rango de (0,49 - 0,499) | |
γ | [kN/m3] | Peso a granel | |
α | [1/K] | Coeficiente de expansión térmica (teniendo en cuenta los efectos de la temperatura) |
El modelo de Drucker-Prager permite, de manera similar al modelo de Mohr-Coulomb, realizar el análisis de estabilidad. Se pueden realizar tanto el análisis de estabilidad de taludes estándar como el análisis de estabilidad dentro de una etapa de construcción determinada. En ambos casos, esta tarea se resuelve reduciendo gradualmente los parámetros de resistencia al corte c, φ introduciendo el parámetro de reducción ζ tal que
![]()
donde c, φ son los parámetros de resistencia al corte reales y cd, φd son los parámetros reducidos. El factor de seguridad FS se obtiene entonces mediante
![]()
De manera similar reducimos el ángulo de dilatación ψ siempre que ψ ≠ 0.
La implementación del modelo de material Drucker-Prager en el programa FEM GEO5 se describe en detalle en el manual teórico.