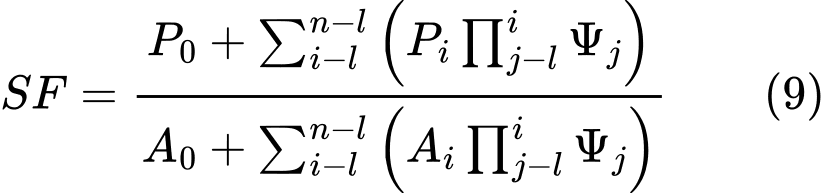Método ITF (Imbalance Thrust Force Method)
O método ITF é um método de verificação dos estados limite. Baseia-se na verificação da equação de equilíbrio das forças atuantes em cada bloco e não considera a equação de equilíbrio de momentos. As premissas consideradas neste método podem ser visualizadas na figura seguinte:
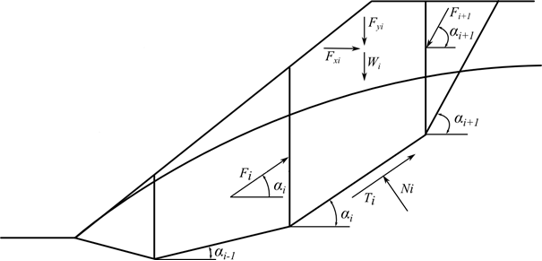Fig. 1 Esquema das forças atuantes - Método ITF
Cada bloco estará sujeito às forças seguintes:
onde: | Wi | - | peso do iésimo bloco, o peso do bloco da parte inferior ao nível freático é determinado considerando o peso volúmico saturado do solo γsat |
Fyi | - | carga vertical sobrante atuante no bloco | |
Fxi | - | carga horizontal sobrante atuante no bloco | |
Fi, Fi+1 | - | forças atuantes entre blocos nas direções dadas pelos ângulos αi e αi+1 |
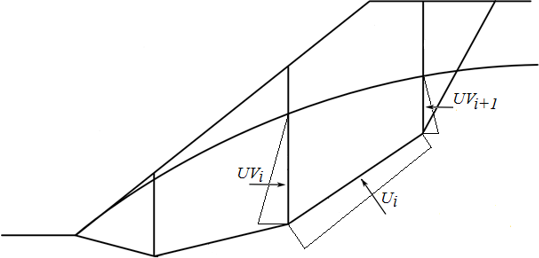Fig. 2 Esquema do empuxo atuante no bloco
Ui | - | resultante do empuxo na superfície de deslizamento | |
UVi,UVi+1 | - | resultante do empuxo nos planos divisores de blocos |
As forças UVi e UVi+1 estão incluídas nas forças horizontais Fxi.
A equação de equilíbrio das forças atuantes na direção normal ao segmento da superfície de deslizamento é dada por:
As forças atuantes no segmento da superfície de deslizamento relacionam-se conforme a seguinte equação:
onde: | φi | - | ângulo de atrito interno do solo |
ci | - | coesão do solo | |
li | - | comprimento do segmento da superfície de deslizamento associado ao iésimo bloco |
A equação de equilíbrio de forças na direção do itésimo segmento da superfície de deslizamento (considerando um ângulo αi) permite obter a força Fi atuante entre blocos:
Introduzindo as Equações (1) e (2) à Equação (3) obtém-se:
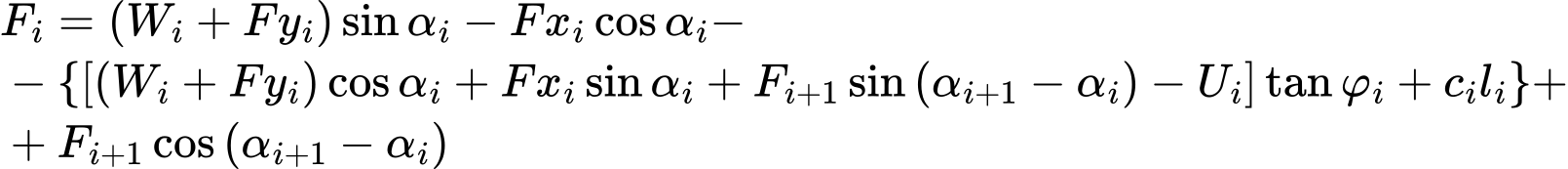
que pode ser desenvolvida de forma a obter a seguinte equação:
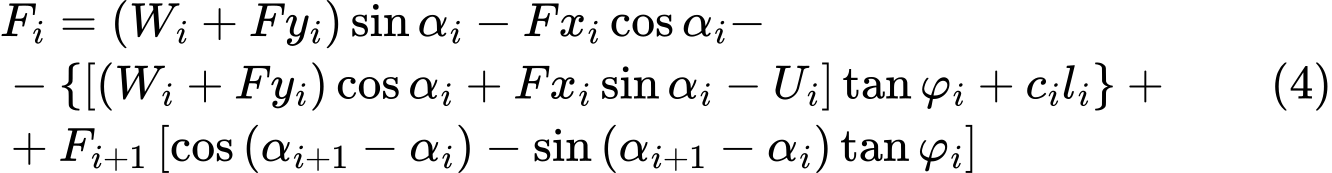
A condição de equilíbrio fica completa com a introdução do fator de segurança FS na análise, dividindo as características do solo c e tanφ por este valor:
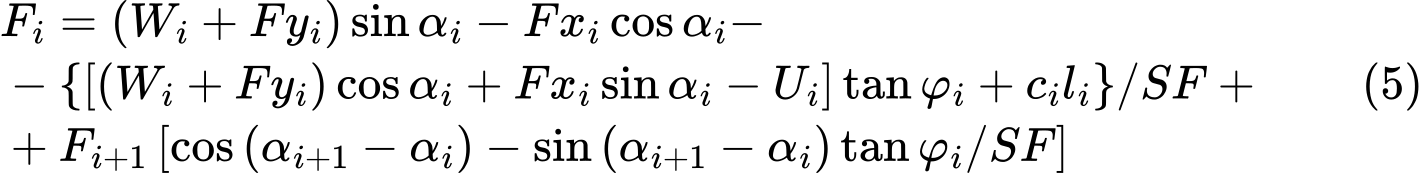
A partir da Equação (5), é possível obter o fator de segurança FS desejado através de um processo iterativo. Este processo desenvolve-se de forma a que a força Fn igual a 0 kN seja aplicada no ponto mais elevado (final) da superfície de deslizamento. As forças Fi atuantes entre blocos são determinadas para um dado fator de segurança FS obtido a partir da Equação (5). Este passo é repetido para vário valores de FS até que se obtenha um valor de FS que permita que a força F0 atuante na base do talude seja igual a 0 kN. Não é assumida nenhuma tensão na superfície de deslizamento. Caso a condição de equilíbrio implique que o valor da força normal Ni seja negativo, o que significa que o solo está carregado à tensão, então o valor desta força é definido como zero na iteração seguinte e a força de cisalhamento Ti atuante num dado segmento é determinada apenas com base na coesão do solo.
O método ITF é muito sensível quanto à forma da superfície de deslizamento. Se a superfície de deslizamento apresentar segmentos com descontinuidades acentuadas, o fator de segurança resultante será mais elevado do que a situação real. Recomenda-se que a diferença na inclinação de segmentos consecutivos da superfície de deslizamento seja inferior a 10°. Isto será verificado automaticamente pelo programa e se esta diferença for superior, o programa emite uma mensagem de aviso a alertar que os resultados poderão estar sobrestimados. Isto não é um problema no caso de superfícies de deslizamento circulares, mas deve ser considerado no caso de superfícies de deslizamento poligonais.
Método ITF - solução explícita
A solução explícita do método ITF apresenta uma forma alternativa para a introdução do fator de segurança na análise. A solução matemática não implica iterações e o fator de segurança resultante é calculado diretamente. Com esta aproximação, o fator de segurança obtido é, normalmente, mais elevado do que a situação real, sendo que esta solução poderá ser desvalorizada, especialmente em casos de superfícies de deslizamento poligonais com grande variância na inclinação entre segmentos consecutivos.
A solução consiste na introdução do fator de segurança FS à Equação (4), de forma a que as componentes ativas das forças sejam multiplicadas por este fator, isto é, as componentes que atuam na direção do deslizamento. Assim, o equilíbrio das forças pode ser escrito da seguinte forma:
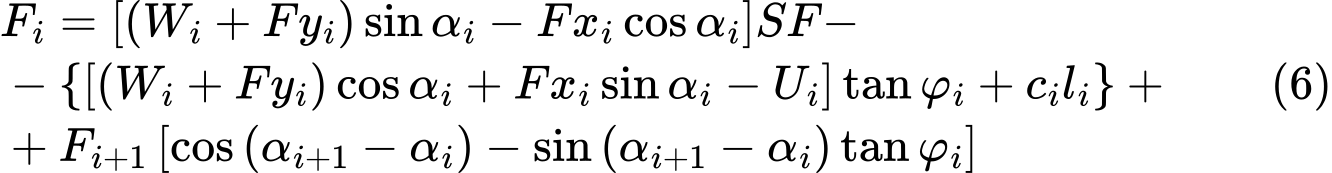
Para clarificar, a componente das forças ativas serão apresentadas como:
e a componente das forças passivas como:
e, ainda, a seguinte função auxiliar:
A Equação (6) pode, então, ser escrita de forma simplificada:
O próximo passo consiste na introdução da força conhecida Fn=0 de modo a ser possível escrever as seguintes expressões para as forças atuantes entre blocos F:
Etc….
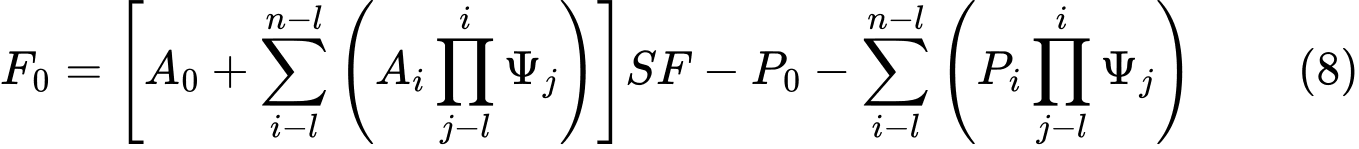
Uma vez que a força atuante no ponto de origem inferior da superfície de deslizamento deve ser igual a 0 kN, obtém-se a expressão final para o cálculo do fator de segurança FS:
