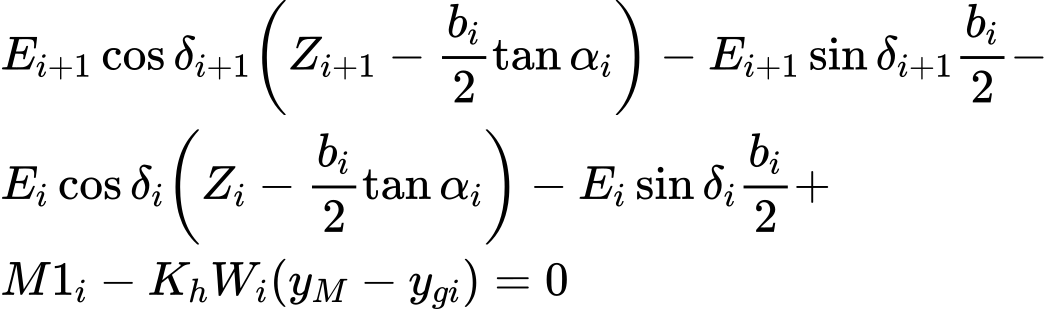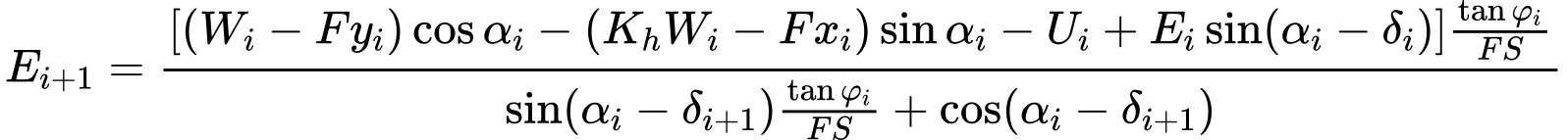Morgenstern-Price
El método Morgenstern-Price es es un método general de cortes realizados en la base del equilibrio límite. Debe satisfacer el equilibrio de fuerzas y momentos actuando en bloques individuales. Los bloque son creados dividiendo el suelo sobre la superficie terrestre dividiendo planos. Las fuerzas actuando en bloques individuales se muestran en la siguiente figura.
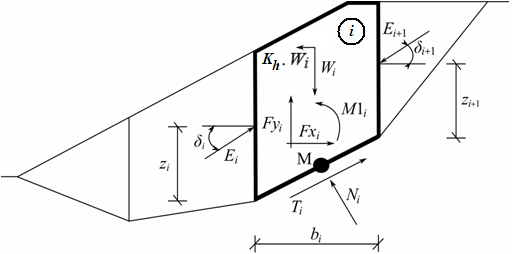Esquema estático – Método Morgenstern-Price
Cada bloque se asume para contribuir a la misma fuera como en el método Spencer. Los siguientes supuestos se introducen en el método Morgenstern-Price para calcular el equilibrio límite de las fuerzas y momento de los bloques individuales:
- Los planos divididos entre bloques son siempre verticales
- La línea de acción de peso del bloque Wi pasa por el centro del segmento ith de la superficie de deslizamiento representada por el punto M
- La fuerza normal Ni actúa en el centro del segmento ith de la superficie de deslizamiento, en el punto M
- La inclinación de las fuerzas Ei que actúan entre los bloques es diferente en cada bloque (δi) al punto extremo de la superficie de deslizamiento δ = 0
La única diferencia entre el método Spencer y el método Morgenstern-Price se ve en la lista de supuestos superior. La elección de los ángulos de inclinación δi de las fuerzas Ei actuando entre los bloques se realiza con la ayuda de la función Half-sine – una de las funciones en la siguiente figura es elegida en forma automática. La elección de la forma de la función tiene una influencia mínima en el resultado final, pero una elección adecuada puede mejorar la convergencia del método. El valor funcional de la función Half-sine f(xi) en el punto limite xi multiplicado por el parámetro λ da como resultado el valor de la inclinación del ángulo δi.
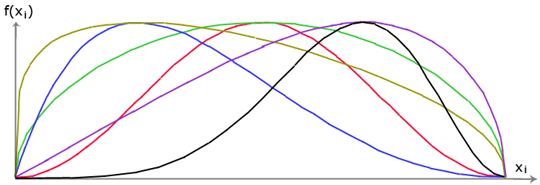Función Half-sine
La solución adopta la expresión (1) – (5),mostrando el método Spencer, es decir:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
- (1) Relación entre el valor de la tensión efectiva y tensión total de la fuerza normal actuando en la superficie de deslizamiento
- (2) Condición de Mohr-Coulomb representa la relación entre la fuerza normal y la fuerza de corte en un segmento dado de la superficie de deslizamiento (Ni a Ti)
- (3) Fuerza de la ecuación de equilibrio en la dirección normal del segmento ith de la superficie de deslizamiento
- (4) Fuerza de la ecuación de equilibrio a lo largo del segmento ith de la superficie de deslizamiento
- (5) Momento de la ecuación de equilibrio sobre el punto M
Modificando las fuerzas de las ecuaciones (3) y (4) se obtiene la siguiente fórmula recursiva:
| (6) |
Este fórmula permite calcular todas las fuerzas Ei actuando entre los bloques para un valor dado de δi y SF. Esta solución asume que en el origen de la superficie de deslizamiento el valor E es conocido e igual a E1 = 0.
Adicionalmente la fórmula recursiva (7) sigue la ecuación de momento de equilibrio (5) como:
| (7) |
Ésta fórmula permite calcular todos los brazos zi de las fuerzas actuando entre los bloques para un valor dado de δi, conociendo el valor del lado izquierdo en el origen de la superficie de deslizamiento, donde z1 = 0.
El factor de seguridad SF es determinado empleando el siguiente proceso de interacción:
- Los valores iniciales de los ángulos δi se determinan según la función Half-sine (δi = λ* f(xi)).
- El factor de seguridad SF para los valores dados de δi deduce de la ecuación (6), asumiendo el valor de En+1 = 0 en el extremo de la superficie de deslizamiento.
- El valor de δi está dado por la ecuación (7) utilizando los valores de Ei determinados en el paso previo con el requisito de tener el momento en el último bloque igual a cero. Los valores funcionales de f(xi) son los mismos todo el tiempo durante la iteración, solo se itera el parámetro de λ. La ecuación (7) no provee el valor de zn+1 ya que éste es igual a cero. Éste valor se satisface con la ecuación de momento de equilibrio (5).
- El paso 2 y 3 se repiten hasta que el valor de δi (parámetro λ) no cambia.
Es necesario evadir las soluciones inestables para que el proceso de iteración sea exitoso. Estas inestabilidades ocurren cuando toma lugar la división por cero en la expresión (6) y (7). En la ecuación (7) dividir por cero se encuentra por δi = π/2 o δi= -π/2. Por lo que, el valor del ángulo δi debe ser encontrado dentro del intervalo (-π/2 ; π/2).
La división por cero en la expresión (6) aparece cuando:
Otra comprobación para prevenir inestabilidad numérica es la verificación de parámetros mα – se satisface siguiendo las siguiente condición.
Por lo tanto, antes de ejecutar la iteración es necesario encontrar el valor crítico mas alto de SFmin que satisfaga las condiciones antes mencionadas. Los valores por debajo de éste valor crítico SFmin se encuentran en un área de solución inestable, por lo que la iteración comienza configurando SF a un valor por encima de SFmin y todos los valores resultantes de SF de las iteraciones ejecutadas son mayores a SFmin.
Generalmente los métodos rigurosos convergen mejor que los métodos simples (Bishop, Fellenius). Ejemplos con problemas convergentes incluyen dos secciones de superficie de deslizamiento empinada, geometría compleja, salto significativo en sobrecargas etc. Si no se obtiene resultado, recomendamos un pequeño cambio en los datos de entrada, ejemplo: superficie de deslizamiento menos empinada, ingreso de más puntos dentro de la superficie de deslizamiento, etc. o utilizar alguno de los métodos simples.
Bibliografía:
Morgenstern, N.R., and Price, V.E. 1965. The analysis of the stability of general slip surfaces. Géotechnique, 15(1): 79–93.
Morgenstern, N.R., and Price, V.E. 1967. A numerical method for solving the equations of stability of general slip surfaces. Computer Journal, 9: 388–393.
Zhu, D.Y., Lee, C.F., Qian, Q.H., and Chen, G.R. 2005. A concise algorithm for computing the factor of safety using the Morgenstern–Price method. Canadian Geotechnical Journal, 42(1): 272–278.